技术干货分享 | 高纯度液体中颗粒污染的数据分析技术

高纯度液体中颗粒污染的数据分析技术

粒子量测为一连续状态的分析，为了判断数据的可靠度，需要以不同分析工具判读数据之合理性，分析工具包含：时间作图、粒径分析、Poisson统计分析、傅立叶分析，透过正确的分析工具以确保量测稳定性。

知 粒子量测名词定义

首先，在开始量测之前，必须先了解粒子量测的名词定义。使量测能得到稳定且再现度高的结果。

• 样品时间间距：每一笔数据所间隔的时间

• 感度：量测时所能探测的最小粒径

• 原始粒子数：量测时所计算的原始数量

• 粒子数浓度：每毫升当中的粒子数量

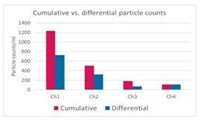
• 粒子数差值 (differential)：每一个单一通道中的粒子数量

• 粒子累积数量 (cumulative)：通道以上的粒子数量加总  

图一、粒子数差值与粒子累积数量的比较

样品间距设定

在选取适合的样品间距之前，需要先确认系统的稳定性。公式一Possion统计公式指出，标准偏差为平均值开根号，需以此公式计算出正确的标准偏差后，才能定义出样品间距。

计算稳定性后，得以计算出标准偏差以及样品间距的关系。当样品间距越小，标准偏差越大，如下方图二所示。

图二、标准偏差与样品间距

时间作图分析

时间作图分析为粒子监控中最常用的工具，能够实时侦测系统中出现的异常粒子行为，并且能够有效的监控过滤器与滤效的关联性，图三显示了时间作图与滤效的比较。

Effect of H2SO4 recirculation/filtration

图三、时间作图与滤效比较

另外，在化学品制备过程中，时常发生因阀件做动而导致粒子的释出，需要严格监控以确保化学质量，下方图四显示了如何以粒子计数器监控异常的阀件做动行为。

Tool activity in NH4OH chemical distribution system

Valve actuations in UPW

图四、监控阀件做动行为

粒径分布分析

粒径分布分析为量测行为判断最常用的方法，透过计算能换算出粒径分布的斜率，因而分析量测的可靠度。如图五所示，异常的粒径分布指出50nm的滤效不佳。

图五、以粒径分析监控滤效

图六为另外一个因异常而导致粒径分布异常的例子。当气泡发生时，导致粒径分布的斜率更平。

图六、气泡导致粒径分布异常

Poisson统计分析

Poisson统计分析定义为在一给定的时间区间中，异常事件发生的可能性分布，需要建立以下几个假设。

• 事件机率为随机发生

• 事件之间彼此独立

• 平均发生几率为常数

• 事件发生的几率与时间的增加成正比

公式二显示了DFP(deviation from Poisson)的计算方法，其中σ代表量测标准偏差，λ1/2为Poisson所定义的的标准偏差。

图七为在UPW系统中的DFP，其中σ=1.25，λ=1.34。经过计算后，DFP = 8%，由此例可以得知，此UPW处于正常且稳定的系统条件。

Particles larger than 20nm in UPW

Frequency Distribution

图七、UPW系统DFP结果

傅立叶变换分析

传统的粒径时间绘图为粒子数与时间的关系，在化学品系统中，经常发生因帮浦/阀件做动而产生的周期性行为，傅立叶变换提供了将周期性量化的工具。图八显示了如何将粒子时间绘图转换成傅立叶频域分析。

图八、傅立叶变换分析

图九为傅立叶变换的实际范例，在硫酸系统中系统发生周期性的扰动，经过傅立叶变换后可以计算出异常事件发生频率为7次/天，因此可计算出周期为200分钟。

图九、硫酸系统傅立叶变换分析

本文通过粒子计数的实际案例，提供了实际能验证量测质量的工具，此方法能够为用户提供以下几个层面的改善。

• 连续性/实时性的20nm粒子监控

• 粒径分布分析来验证量测的正确性

• Poisson统计分析验证系统的稳定性

• 傅立叶变换分析来验证系统的周期性事件

以上方法对于粒子监测的使用者提出了有效且实时的分析方法，使每次的样品搜集能够得到优化的结果。如您想了解更多相关内容或有任何疑问，请通过下方任一方式与我们取得联系。